Modern Portfolio Theory provides a solid foundation for portfolio construction, but it has limitations that become apparent when you start using it in practice. Many institutional investors and portfolio managers have discovered that MPT, on its own, often produces portfolio recommendations that don't align well with their market views or practical constraints.
That's where the Black-Litterman model comes in. Developed by Fischer Black and Robert Litterman at Goldman Sachs in 1990, the Black-Litterman model addresses several key shortcomings of traditional MPT while maintaining mathematical rigor. It's become a standard tool for large institutional investors, mutual funds, and insurance companies managing complex portfolios.
In this guide, we'll explore how the Black-Litterman model works, when to use it, and how it compares to other portfolio optimization approaches. If you're new to portfolio optimization, we recommend starting with our complete guide to portfolio optimization and Modern Portfolio Theory, which covers the foundational concepts. For practical implementation in Excel, check out our step-by-step Excel implementation guide.
Moving Beyond Traditional MPT
Modern Portfolio Theory revolutionized investment management, but practical experience revealed some challenges when applying it to real-world portfolio construction.
The Problem with Pure MPT
The core issue is that MPT relies entirely on historical data to estimate expected returns, volatilities, and correlations between assets. The model looks backward, using past performance to predict future results. But as every investment disclosure warns, past performance doesn't guarantee future results.
This creates several practical problems:
Extreme portfolio recommendations: MPT often suggests concentrated positions in assets that have recently performed well. The model might recommend putting 40% or 50% of your portfolio in a single asset class simply because it had high historical returns and low historical correlation with other assets.
Ignores investor knowledge: Portfolio managers often have insights, research, and views about future market conditions. Maybe you believe emerging markets are poised to outperform, or you think interest rates will rise faster than markets expect. Traditional MPT has no way to incorporate these forward-looking views.
Unstable allocations: Small changes in input data can produce dramatically different portfolio recommendations. Update your data by one month and your optimal allocation might shift significantly. This instability makes it difficult to implement MPT recommendations consistently.
Counter-intuitive results: Sometimes MPT recommends allocations that just don't make sense given current market conditions. It might suggest heavy exposure to an asset class that's clearly overvalued, simply because historical data suggests it has attractive risk-return characteristics.
These limitations don't mean MPT is wrong. The theory is sound. But it needs enhancement to work well in practice, especially for large, complex portfolios where small allocation errors can have significant consequences.
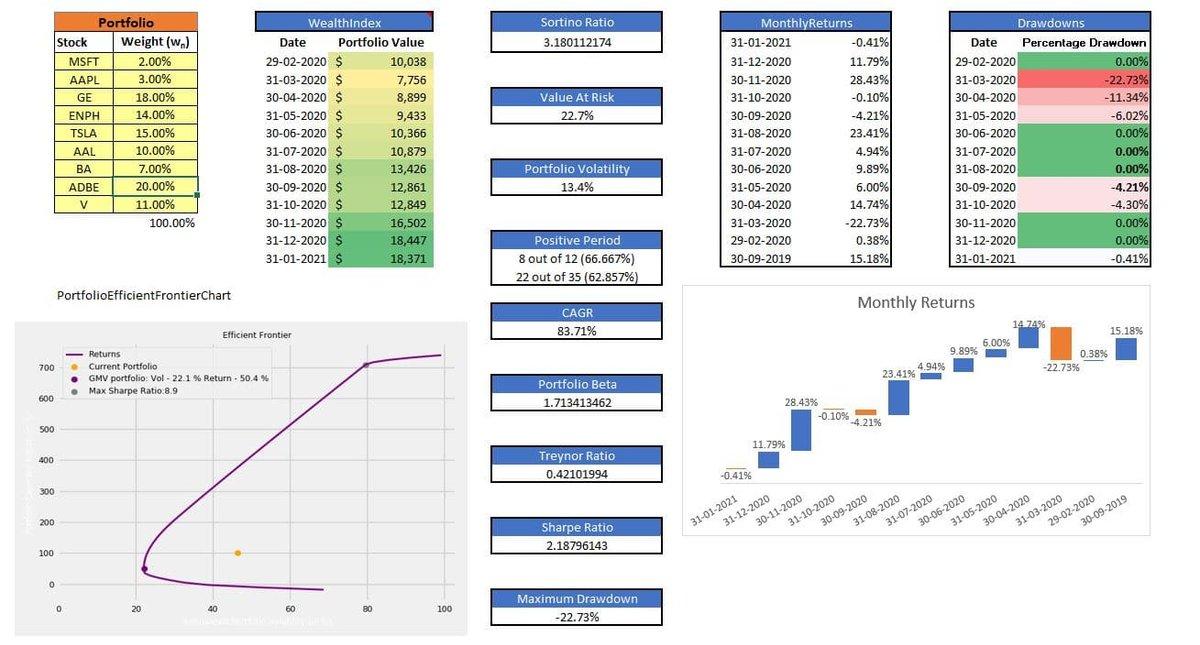
Advanced Portfolio Analytics
The Black-Litterman Model Explained
The Black-Litterman (BL) model improves upon MPT by combining market equilibrium with investor views. Instead of relying only on historical data, the BL model starts with market-implied returns and then adjusts them based on specific views about how certain assets will perform.
The History and Development
Fischer Black and Robert Litterman developed the model at Goldman Sachs in 1990 to solve practical problems they encountered when applying MPT to institutional portfolios. They needed a framework that could incorporate the firm's research and market views while maintaining the mathematical rigor of portfolio theory.
The model they created represents an elegant synthesis of three important concepts:
Capital Asset Pricing Model (CAPM): Provides the framework for understanding how assets should be priced in equilibrium based on their systematic risk.
Modern Portfolio Theory: Supplies the mathematical tools for portfolio optimization and the concept of the efficient frontier.
Bayesian Statistics: Offers a principled way to combine prior beliefs (market equilibrium) with new information (investor views) to form updated expectations.
This combination creates a more stable and intuitive optimization framework than pure MPT while still producing portfolios that lie on the efficient frontier.
How Black-Litterman Improves Upon MPT
The key insight of the Black-Litterman model is to reverse the typical optimization process. Instead of using historical returns to find optimal portfolios, the model starts with current market weights (the market portfolio) and asks: "What returns would justify these weights?"
This produces what's called the "equilibrium return" for each asset. These equilibrium returns represent the market's collective expectation. They're inherently more stable than historical average returns because they're based on current prices and market capitalizations rather than backward-looking performance data.
Once you have equilibrium returns, you can then express views about how specific assets might deviate from equilibrium. For example:
"I believe U.S. large-cap stocks will outperform by 2% annually over the next 3-5 years."
"I expect emerging market bonds to underperform developed market bonds by 1%."
"I'm neutral on real estate but believe commodities will underperform by 3%."
The Black-Litterman model takes these views, combines them with the equilibrium returns using Bayesian methods, and produces a new set of expected returns. These "posterior" expected returns then feed into a standard mean-variance optimization to generate portfolio weights.
The beauty of this approach is that it produces more intuitive, stable portfolios that reflect both market consensus and your specific insights.
How the Black-Litterman Model Works
Let's walk through the mechanics of the Black-Litterman model to understand how it transforms market data and investor views into optimal portfolio weights.
Starting with Market Equilibrium
The model begins by calculating the market portfolio, which represents the aggregate holdings of all investors. For a global equity portfolio, this might be weighted by market capitalization. U.S. stocks might represent 60% of global equity markets, European stocks 20%, Japanese stocks 10%, and emerging markets 10%.
The model then uses these market weights to back out implied equilibrium returns. This process assumes the market portfolio is optimal (a reasonable starting point given that it represents the collective wisdom of all market participants). The equilibrium returns are the expected returns that would make this market portfolio lie on the efficient frontier.
These equilibrium returns are much more stable than historical returns. They change gradually as market weights shift, rather than jumping around based on recent performance.
Adding Investor Views
Once you have equilibrium returns, you express views about specific assets or asset classes. Views can be:
Absolute: "I expect U.S. stocks to return 8% annually."
Relative: "I expect U.S. stocks to outperform European stocks by 3%."
Partial: You can express views on some assets while remaining neutral on others.
Importantly, you also specify your confidence in each view. A high-confidence view (based on thorough research and strong conviction) gets more weight in the final portfolio. A low-confidence view (perhaps based on a hunch or limited data) gets less weight.
This confidence weighting is crucial. It prevents you from overreacting to uncertain views while still allowing strong convictions to meaningfully influence the portfolio.
Combining Views with Equilibrium
The model uses Bayesian statistics to blend your views with the equilibrium returns. Think of equilibrium returns as your "prior" (what you'd believe if you had no special information) and your views as "updates" to that prior.
The result is a set of posterior expected returns that reflect both market consensus and your specific insights. Assets where you have bullish views get higher expected returns than equilibrium would suggest. Assets where you're bearish get lower expected returns.
Calculating Optimal Portfolio Weights
Finally, these posterior expected returns feed into a standard mean-variance optimization, just like in traditional MPT. The optimization finds the portfolio on the efficient frontier that offers the best risk-return tradeoff given your updated return expectations.
Because the starting point (equilibrium returns) is stable and the adjustments (your views) are explicitly stated and confidence-weighted, the resulting portfolios tend to be much more reasonable and stable than pure MPT would produce.
When to Use Black-Litterman
The Black-Litterman model isn't necessary for every portfolio. It adds complexity, and that complexity is only justified in certain situations.
Ideal Use Cases
Institutional portfolios: Large pension funds, endowments, and foundations managing hundreds of millions or billions of dollars benefit most from Black-Litterman. At that scale, modest improvements in allocation efficiency can translate to millions of dollars in additional returns.
Mutual funds and hedge funds: Professional asset managers often have strong research capabilities and market views. Black-Litterman provides a disciplined way to translate research insights into portfolio positions without overriding market wisdom entirely.
Insurance company asset allocation: Insurance companies must match assets to long-term liabilities while managing risk carefully. The stability and rigor of Black-Litterman make it attractive for this application.
Multi-asset portfolios: When allocating across many asset classes (stocks, bonds, real estate, commodities, private equity, etc.), Black-Litterman's ability to handle complex relationships and incorporate partial views becomes particularly valuable.
Strategic asset allocation: For long-term strategic decisions about portfolio structure, Black-Litterman's focus on stable equilibrium returns is more appropriate than backward-looking historical returns.
When Simpler Approaches Work Better
Not every investor needs Black-Litterman. The model may be overkill if:
You're managing a small portfolio: For individual investors or small portfolios (under $1 million), the additional complexity rarely justifies the marginal improvement over simpler diversification approaches.
You lack strong views: If you're essentially a passive investor who believes in market efficiency, there's little reason to deviate from market-cap-weighted index funds. Black-Litterman is designed to incorporate views, so without them, you're better off with simpler approaches.
You're investing in a single asset class: If you're only selecting stocks or only building a bond portfolio, traditional optimization methods or fundamental analysis may be more appropriate.
Time and resources are limited: Implementing Black-Litterman properly requires time to develop views, assess confidence levels, and set up the mathematical framework. If you don't have those resources, stick with simpler methods that you can implement well rather than complex models you'll implement poorly.
Black-Litterman Limitations and Considerations
Like any model, Black-Litterman has limitations and assumptions that can cause problems if you're not careful.
The Normality Assumption
The model assumes asset returns follow a normal distribution. In reality, returns often have "fat tails," meaning extreme events occur more frequently than a normal distribution would predict. The 2008 financial crisis is a stark example. Models based on normal distributions underestimated the probability of severe market declines.
This means Black-Litterman, like MPT, can underestimate tail risk. You need to supplement the model with stress testing and scenario analysis to understand how your portfolio might perform during extreme events.
Market Equilibrium Challenges
The model's foundation rests on defining the market portfolio correctly. But what exactly is "the market"? Should it include only publicly traded securities? What about real estate, private equity, commodities, and other assets?
In practice, many risky assets aren't easily included in the market portfolio calculation. This makes it challenging to accurately reproduce optimal allocations in the real world. Different definitions of the market portfolio can lead to different equilibrium returns and, ultimately, different recommended allocations.
Sensitivity to Investor Inputs
All portfolio optimization models depend on inputs, but Black-Litterman is especially sensitive because it includes an additional layer: your views and confidence levels.
Small changes in how you express views or assess confidence can meaningfully change the resulting portfolio. This isn't necessarily bad, it's actually a feature that allows the model to incorporate your insights. But it means you need to be thoughtful and consistent in how you formulate views.
The Risk of Biased Views
The model gives you the power to deviate from market equilibrium based on your views. This is valuable when your views are based on genuine insight and careful research. But it's dangerous when views are based on overconfidence, biases, or incomplete analysis.
Consider the risk of overly optimistic views. During the late 1990s tech bubble, many investors had very bullish views on technology stocks. A Black-Litterman model would have translated those bullish views into heavy tech allocations. When the bubble burst, those portfolios suffered enormous losses.
The model amplifies both insight and error. If your views are well-founded, Black-Litterman helps you profit from them. If your views are wrong, it ensures those errors materially impact your portfolio.
AI and Machine Learning in Portfolio Optimization
While the Black-Litterman model represents a major advance over traditional MPT, the investment management industry continues to evolve. Artificial intelligence and machine learning are increasingly being applied to portfolio optimization, offering new approaches to the age-old challenge of balancing risk and return.
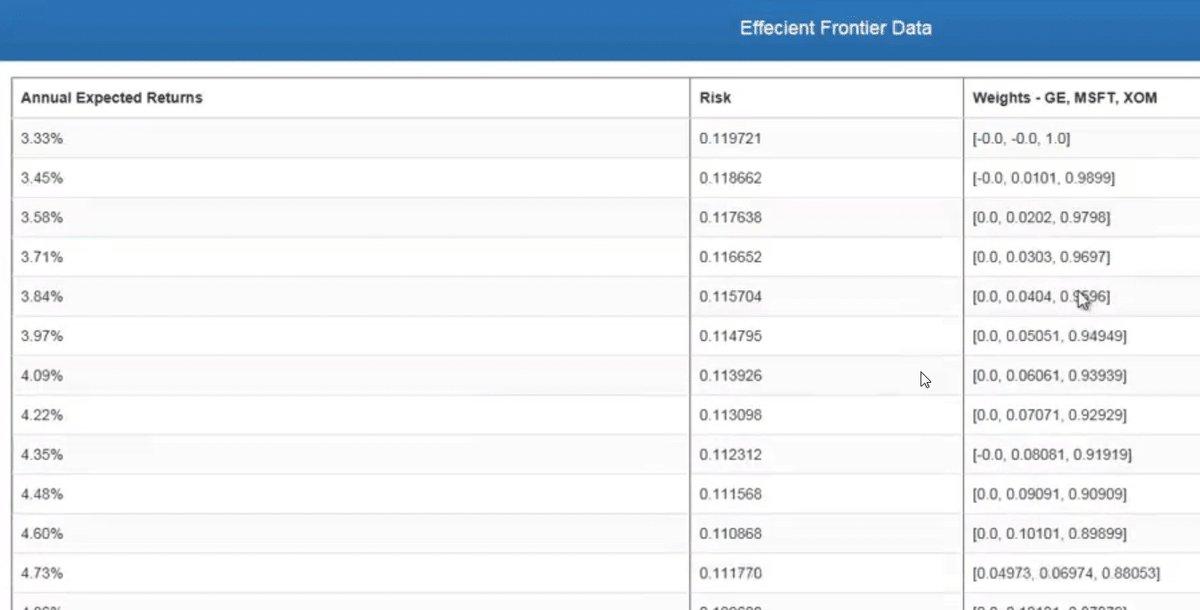
Modern Portfolio Theory
How AI Enhances Portfolio Optimization
Pattern Recognition: Machine learning algorithms can identify complex patterns in market data that humans might miss. They can detect subtle relationships between economic indicators, market sentiment, and asset returns that inform better allocation decisions.
Alternative Data Integration: AI systems can process vast amounts of alternative data (satellite imagery, social media sentiment, credit card transactions, etc.) to generate insights about future asset performance. This information can enhance traditional financial analysis.
Dynamic Rebalancing: AI can continuously monitor portfolios and market conditions, making real-time adjustments that would be impossible for human portfolio managers. This can help maintain optimal allocations as market conditions change.
Risk Management: Machine learning models can identify emerging risks and stress-test portfolios against scenarios that haven't occurred historically. This helps address one of the key limitations of traditional models that rely on historical data.
Algorithmic Trading and Portfolio Management
Algorithmic trading systems represent one of the most mature applications of AI in portfolio management. These systems can:
Execute Complex Strategies: Algorithms can implement sophisticated trading strategies across multiple assets simultaneously, ensuring optimal execution while minimizing market impact.
Optimize Transaction Costs: AI can determine the best times and methods for executing trades, reducing slippage and transaction costs that can erode portfolio returns.
Manage Multiple Constraints: Algorithms can handle complex constraint systems (risk limits, sector exposures, ESG requirements) while still optimizing for return.
Data-Driven Investing
AI enables truly data-driven investing approaches that go beyond what's possible with traditional methods:
Sentiment Analysis: Natural language processing can analyze news, earnings calls, and social media to gauge market sentiment and predict short-term price movements.
Factor Discovery: Machine learning can identify new factors that drive returns, potentially uncovering sources of alpha that haven't been widely exploited.
Regime Detection: AI systems can identify when market conditions are changing, allowing portfolios to adapt to new environments more quickly than traditional approaches.
Risk Management Enhancement
AI provides powerful tools for managing portfolio risk:
Real-Time Risk Monitoring: AI systems can continuously calculate portfolio risk metrics and alert managers to emerging threats.
Tail Risk Assessment: Machine learning models trained on extensive historical data can better estimate the probability of extreme events.
Correlation Breakdown Detection: AI can identify when historical correlation patterns are breaking down, which is crucial during market crises when diversification benefits often disappear.
Practical Implementation Considerations
Whether you're implementing Black-Litterman or exploring AI-driven approaches, several practical considerations are crucial for success.
Building the Infrastructure
Data Quality: All sophisticated portfolio optimization approaches require high-quality, timely data. Garbage in, garbage out applies especially strongly to quantitative portfolio management.
Technology Platform: You need computing infrastructure capable of handling the mathematical complexity. This might range from advanced Excel models to specialized portfolio optimization software to cloud-based AI platforms.
Risk Management Framework: Advanced optimization techniques can generate complex portfolios that require sophisticated risk management. You need systems to monitor and control the risks these portfolios create.
Human Judgment vs. Quantitative Models
The most successful portfolio optimization approaches combine quantitative rigor with human judgment:
Model Oversight: Even the most sophisticated models need human oversight. Experienced portfolio managers can spot when model outputs don't make sense and need adjustment.
Scenario Planning: Quantitative models should be supplemented with scenario analysis and stress testing that considers situations the models might not handle well.
Behavioral Considerations: Models often ignore the behavioral aspects of investing. Human judgment is crucial for ensuring that optimization results can be implemented and maintained through different market cycles.
Starting Simple and Scaling Up
Most investors are better served starting with simpler approaches and gradually adding complexity:
Master the Basics: Before jumping to Black-Litterman or AI approaches, ensure you have a solid understanding of basic portfolio optimization principles.
Validate Models: Any new optimization approach should be thoroughly tested before being implemented with real money. Backtesting and simulation can help identify potential problems.
Gradual Implementation: Consider implementing new techniques with a small portion of your portfolio first, gradually expanding as you gain confidence and experience.
Choosing the Right Optimization Approach
So when should you use traditional MPT, when should you use Black-Litterman, and when should you stick with simple diversification?
Basic Diversification
For most individual investors, simple diversification based on target-date funds or model portfolios works well. Spread your investments across stocks and bonds, diversify within each category, rebalance periodically, and focus on keeping costs low.
This approach is appropriate when:
- Your portfolio is relatively small
- You don't have strong, well-researched market views
- You prefer simplicity and transparency
- You believe markets are generally efficient
Simple diversification, consistently applied, beats complex strategies poorly implemented.
Traditional MPT Optimization
Standard mean-variance optimization using historical data works when:
- You're managing mid-sized portfolios ($1M to $50M)
- You have good historical data for the assets you're considering
- You're comfortable with backward-looking assumptions
- You want more precision than simple diversification but aren't ready for Black-Litterman complexity
If you go this route, implement the Excel-based portfolio optimization techniques we discussed previously. They give you professional-grade analytics while keeping the process transparent and manageable.
Black-Litterman Model
Black-Litterman makes sense when:
- You're managing large, complex portfolios (typically $50M+)
- You have a research team or process that generates genuine market insights
- You're willing to invest time in learning the framework and implementing it properly
- Portfolio stability is important (minimizing turnover and trading costs)
- You're making strategic asset allocation decisions with multi-year time horizons
The model works best in institutional settings where the infrastructure exists to support it properly.
AI-Driven Approaches
AI and machine learning techniques are most appropriate when:
- You're managing very large portfolios (typically $100M+)
- You have access to significant computing resources and data
- You have quantitative expertise on your team
- You're comfortable with "black box" elements in your process
- You can dedicate substantial resources to model development and maintenance
Hybrid Approaches
Many investors use hybrid approaches that blend different methods:
MPT with constraints: Use traditional mean-variance optimization but add constraints that prevent extreme allocations. For example, no asset class can exceed 30% or fall below 5%.
Black-Litterman with simple views: Use the Black-Litterman framework but only express a few high-conviction views rather than trying to have opinions on every asset.
Periodic reoptimization: Use simple allocation rules most of the time but periodically (annually or semi-annually) run more sophisticated optimization to ensure you're not drifting too far from optimal.
The key is matching the sophistication of your approach to your resources, expertise, and actual needs. More complex isn't always better.
Putting It All Together
Portfolio optimization has come a long way from Harry Markowitz's original 1952 paper. We now have a range of tools and techniques, from simple diversification to sophisticated models like Black-Litterman to cutting-edge AI approaches.
The Black-Litterman model represents an important advance for investors who need to incorporate market views into portfolio construction while maintaining rigor and stability. It addresses real limitations of traditional MPT and has proven valuable for institutional investors managing large, complex portfolios.
AI and machine learning offer exciting possibilities for the future, but they're not yet ready for widespread adoption by individual investors or smaller institutions. The technology is rapidly evolving, but it requires significant resources and expertise to implement effectively.
But it's not the right tool for everyone. Most individual investors and many smaller institutions are better served by simpler approaches that they can understand and implement consistently.
Whether you're just starting to explore portfolio optimization fundamentals or ready to implement sophisticated analytics, the key is understanding your options and choosing the approach that fits your situation.
Portfolio optimization isn't about using the most complex model available. It's about finding the right balance between theoretical sophistication and practical implementation. Sometimes that means Black-Litterman. Sometimes it means traditional MPT. And sometimes it means sticking with simple, disciplined diversification.
The best approach is the one you understand well, can implement consistently, and matches the complexity of your portfolio and the sophistication of your decision-making process.
Previous in Series: Portfolio Optimization in Excel: Complete Implementation Guide
Start of Series: Portfolio Optimization & Modern Portfolio Theory: Complete Guide
Series Overview: Portfolio Optimization Series
