Black-Scholes Option Pricing in Excel

Table of Contents

• Introduction
• What is Black Scholes Model?
• Is Black-Scholes still used?
• How to use Black-Scholes model to price options?
• Understanding the Black-Scholes Model with an Excel Example
• How does Black-Scholes Model work with MarketXLS?
  • Syntax
  • Parameters
  • Example
  • Detailed Explanation
  • Extended Functionality
• Summary

Introduction to Black Scholes Excel

Unlocking the Secrets of Option Pricing: The Black-Scholes Model in Excel Ever wondered how traders price options in the financial markets? The Black-Scholes model is your answer. Developed in 1973, this mathematical framework revolutionized how European-style options are priced. From seasoned traders to financial analysts and academics and many in the finance world continue to rely on this powerful tool. In this article, we’ll demystify the Black-Scholes model and show you how to implement it using Excel and make complex calculations simple and accessible.

What is the Black Scholes Model?

The Black-Scholes Model is a mathematical framework for pricing European-style options. Developed by Fischer Black and Myron Scholes in 1973, it revolutionized the field of financial derivatives further, the model provides a formula to calculate the theoretical price of an option based on factors like the current price of the underlying asset, the option’s strike price, time to expiration, risk-free interest rate, and asset volatility. It assumes markets are efficient and follows a geometric Brownian motion. While highly influential, the model has limitations, such as not accounting for dividends or extreme market conditions.

Is Black-Scholes still used?

The Black-Scholes model, introduced in the 1970s, is still widely used in finance, particularly for pricing European-style options. This model has become fundamental to the field of financial economics. Traders, financial analysts, and academics appreciate its relatively straightforward application. However, it has limitations, such as assumptions of constant volatility and a log-normal distribution of asset prices. Despite these drawbacks, its simplicity and historical significance ensure its ongoing relevance. Many financial institutions employ it alongside more complex models to gain diverse perspectives.

How to use Black-Scholes model to price options?

To use the Black-Scholes model to price options, you need several inputs: the stock price, the strike price, time to expiration, risk-free interest rate, and the volatility of the stock to further determine the stock’s initial price and the option’s strike price. Next, estimate the time remaining until the option expires. Obtain the current risk-free interest rate and the stock’s volatility from market data. With these inputs, calculate the option’s d1 and d2 values using the Black-Scholes formulas. Plug these into the cumulative distribution function of the standard normal distribution. Finally, these results are used to find the option’s theoretical price by applying the model’s equation. The Black-Scholes model is primarily for European options and assumes constant volatility and risk-free rates. It provides a theoretical price that can be compared to the market price for trading decisions.

Understanding the Black-Scholes Model with an Excel Example

The Black-Scholes model is a fundamental concept in financial mathematics for pricing European-style options. It provides a theoretical estimate of the price of options, allowing traders to make more informed decisions. Let’s walk through an example of how we can implement the Black-Scholes model in Excel.

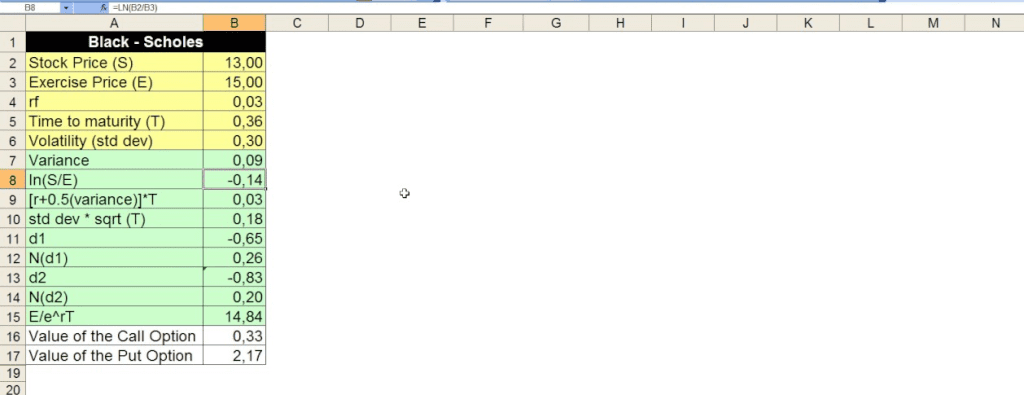
In the given spreadsheet, we have several key inputs and outputs relevant to the Black-Scholes formula:

1. Stock Price (S): The current price of the underlying stock. In this example, it is 13.00.
2. Exercise Price (E): The strike price of the option, which is the price at which the option can be exercised. Here, it is 15.00.
3. Risk-Free Rate (rf): The annual risk-free interest rate, assumed to be 3% (0.03).
4. Time to Maturity (T): The time remaining until the option’s expiration, expressed in years. This example uses 0.36 years.
5. Volatility (σ): The standard deviation of the stock’s returns, indicating its volatility. The value used here is 30% (0.30).
6. Variance (σ²): The square of the volatility, which in this case is 0.09 (0.30²).

Calculations

The spreadsheet performs several intermediate calculations to arrive at the option prices:

• ln(S/E): The natural logarithm of the ratio of the stock price to the exercise price. This gives -0.14.
• [rf + 0.5 * (variance)] * T: This calculates the adjusted interest rate over the period until maturity, resulting in 0.03.
• Standard Deviation * sqrt(T): The standard deviation scaled by the square root of the time to maturity, yielding 0.18.

We use these Intermediate values to compute:

• d1 and d2: Two important values in the Black-Scholes formula calculated as follows:
  • d1=ln(S/E)+(rf+0.5∗σ2)∗Tσ∗T=−0.65d1 = \frac{ln(S/E) + (rf + 0.5 * σ²) * T}{σ * \sqrt{T}} = -0.65d1=σ∗T​ln(S/E)+(rf+0.5∗σ2)∗T​=−0.65
  • d2=d1−σ∗T=−0.83d2 = d1 – σ * \sqrt{T} = -0.83d2=d1−σ∗T​=−0.83
• N(d1) and N(d2): These represent the cumulative distribution function (CDF) values for d1 and d2, which are 0.26 and 0.20 respectively.

Final Option Prices

The spreadsheet then uses these values to calculate the call and put option prices:

• Value of the Call Option: This is calculated using the formula:C=S∗N(d1)−E∗e−rf∗T∗N(d2)C = S * N(d1) – E * e^{-rf * T} * N(d2)C=S∗N(d1)−E∗e−rf∗T∗N(d2)In this example, the value is 0.33.
• Value of the Put Option: This is derived using the put-call parity or directly from:P=E∗e−rf∗T∗N(−d2)−S∗N(−d1)P = E * e^{-rf * T} * N(-d2) – S * N(-d1)P=E∗e−rf∗T∗N(−d2)−S∗N(−d1)Here, the value is 2.17.

How does Black-Scholes Model work with MarketXLS in Excel?

Syntax

=BlackScholesOptionValue(optionSymbol, riskFreeRate, sigma)

Parameters

• optionSymbol: The symbol of the option you are analyzing.
• riskFreeRate: The annual risk-free interest rate, expressed as a percentage.
• sigma: The volatility of the underlying security, expressed as a percentage.

Example

If you want to calculate the Black-Scholes value for an SPY call option with an expiration date of December 16, 2022, a risk-free rate of 2.5%, and a market volatility (sigma) of 20%, you would use:

=BlackScholesOptionValue(“@SPY 221216C00430000”, 2.5, 20)

Prefix “=mxls.” for Excel Online, and Excel on MAC

Detailed Explanation

The Black-Scholes model determines the fair price of European call and put options by considering the following factors:

• The current price of the underlying stock
• The strike price of the option
• The time to expiration of the option
• The volatility of the underlying stock
• The risk-free interest rate

The formula incorporates these factors to provide an estimated fair value of the option, which can help investors make more informed decisions regarding option pricing and trading.

Extended Functionality

An extended version of this function allows for more detailed user inputs:

=BlackScholesOptionValueWithUserInputs(stockPrice, strikePrice, optionType, expiryDate, riskFreeRate, dividendYield, sigma)

Prefix “=mxls.” for Excel Online, and Excel on MAC

Example

=BlackScholesOptionValueWithUserInputs(150, 160, “put”, “2022-12-16”, 2.5, 0, 20)

Prefix “=mxls.” for Excel Online, and Excel on MAC

In this example, 150 is the stock price, 160 is the strike price, “put” is the option type, 2022-12-16 is the expiry date, 2.5% is the risk-free rate, 0 is the dividend yield, and 20% is the volatility.

If you need further assistance or encounter any issues, please email support at support@marketxls.com or call 1-877-778-8358.

Summary

The Black-Scholes model prices European-style options. Developed in 1973, it remains essential in finance. The model uses factors like stock price, strike price, time to expiration, risk-free interest rate, and volatility. You can implement it in Excel using specific formulas. The article guides you through setting up the model in Excel and includes example calculations. The Black-Scholes model calculates option prices using inputs such as stock price, strike price, and others also Excel can simplify these complicated calculations. For example, MarketXLS offers functions to compute theoretical option values using Black-Scholes in Excel.