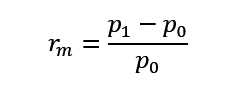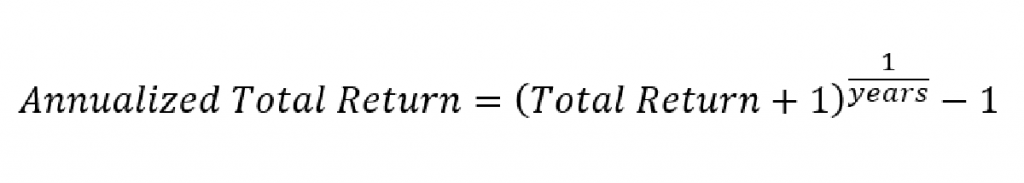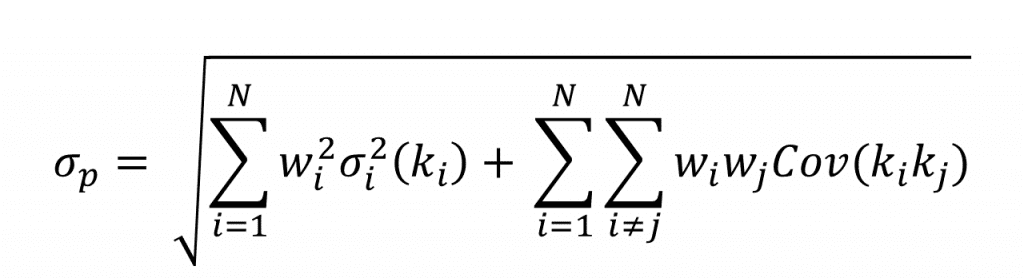Efficient Frontier Using Excel (With Marketxls)

The Efficient frontier using excel is one of the most important financial tools that help an investor compose an investment portfolio with the maximum returns and minimum amount of risk. This article will discuss what it is, how it is then calculated, and how MarketXLS calculates it of your Portfolio.

Contents:

1. What is Efficient frontier
2. Importance of Efficient frontier
3. Optimal Portfolio by Efficient frontier
4. How MarketXLS Calculates Efficient frontier of Portfolio

What is an Efficient frontier?

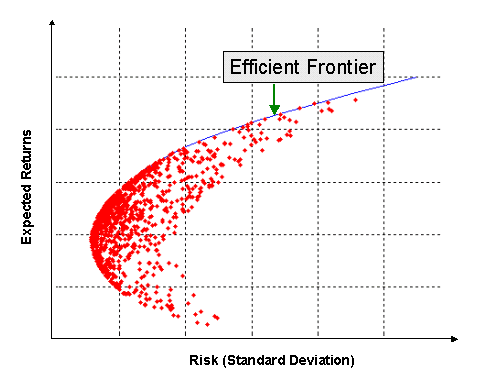
The Efficient frontier, also known as the portfolio frontier, represents the set of efficient portfolios that will give the highest return at each level of risk or the lowest risk for each level of return. The set of efficient portfolios is produced by the combination of different weights to get maximum expected return.

The Efficient frontier is a curve representing a combination of various securities to produce a different level of return.This frontier is formed by plotting the expected return on the y-axis and the standard deviation as a measure of risk on the x-axis.

For building the frontier, there are three crucial factors to be taken into consideration:

1. Expected Return
2. The covariance of one asset’s return to that of another asset.
3. Variance/ Standard Deviation as a measure of the variability of returns known as risk.

The efficient frontier allows investors to understand how a portfolio’s expected returns vary with the amount of risk taken.

Importance of Efficient frontier

This tool helps investors get the most from their investment by analyzing the risk and returns associated with an investment portfolio and assisting them in adjusting their asset allocation accordingly.

It can also help determine if an investor should pull their funds from an investment with a certain amount of risk and return for a similar investment with less risk and the same return. The efficient frontier is important as it minimizes risk while maximizing rewards or returns.

The Optimal Portfolio by Efficient frontier

An optimal portfolio would offer a perfect balance between risk and return. The optimal portfolio contains:

1. Securities with the highest potential returns with an acceptable degree of risk.
2. It features securities with the lowest degree of risk for a certain level of return.
3. Optimal returns tend to lie along the efficient frontier.

A risk-ready investor could choose securities right end of the efficient frontier. Those would likely have a high degree of risk coupled with high potential returns. Meanwhile, securities on the left end of the efficient frontier would be suitable for more cautious investors.

How MarketXLS Calculates Efficient frontier of your Portfolio

MarketXLS® completely automates the process of calculating the Efficient frontier using excel to get the optimal portfolios which tend to lie along the efficient frontier.

The following inputs are required to be entered by the investor:

1. Symbol of the asset: Enter the ticker under which the security in your Portfolio is traded.
2. Weight of the asset in your Portfolio: Enter the percentage weight of each security, as shown below.

Input:

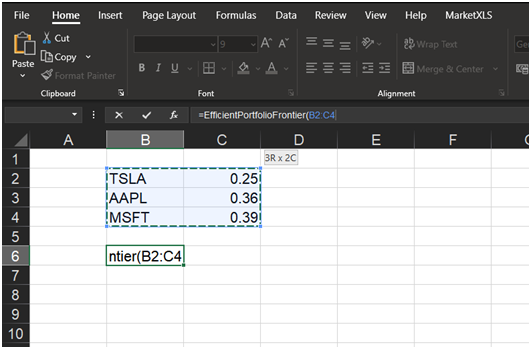
Output:

Optional Fields:

Risk-free-rate(Rf):

To account for individuality in investor outlook, we make sure to give you the flexibility of determining what Mar/Rf you think is most viable. Default value: MarketXLS assumes a Mar/Rf of 0% by default to calculate the ratio.

Months under observation:

To determine how many months you want to utilize retrospectively to arrive at your calculation, you may input the number of months you feel best, given that all the securities in your Portfolio have existed long enough to have data for those periods. Default Value: In the absence of any user input, MarketXLS uses the data for the preceding 12 months from the date of the query.

Number of Points:

This refers to the number of points for which data is calculated for plotting the frontier. Default Value: MarketXLS calculates 100 points of data by default. 

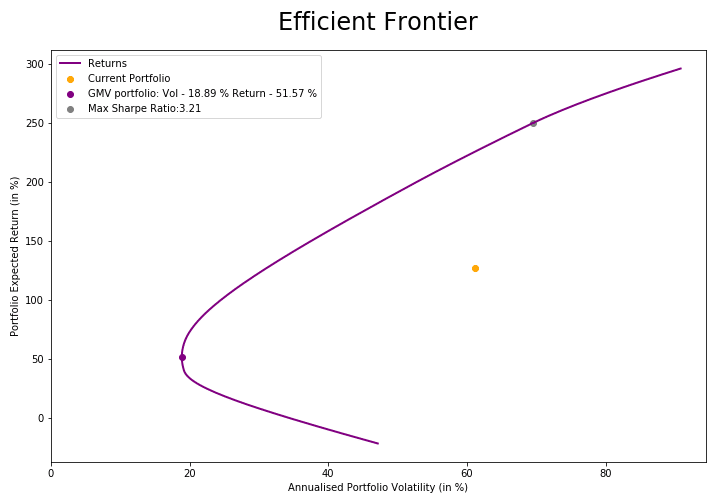
The  GMV Portfolio:

The global minimum variance portfolio (GMV portfolio), is the portfolio with the lowest possible standard deviation (risk) out of all possible levels of expected return.

Calculation:

The following is how the MarketXLS add-in calculates the Efficient frontier for your Portfolio, one may note, that this also serves as an explanatory step-by-step guide for an n-asset portfolio as to how to calculate the Efficient frontier.

Method to calculate average monthly return is same for both types as follows:

1. Monthly Return Calculation for Each Asset in Portfolio:

Where:

Note: To maintain consistency with theory in this regard, Close Price is a security’s Adjusted Close (Close prices adjusted for dividends and splits) of the last day of a given month, and the Open Price is the Adjusted Close price for the last day of the previous month.

2. Portfolio Monthly Return Calculation:

Portfolio return for a given month is calculated as follows:

Where:

This is repeated for all the months under consideration.

3. Determining Highest and Lowest Possible Expected Return on a Portfolio:

The individual return of every asset in the portfolio is determined by taking the mean of periodic returns for every asset and annualising the same to arrive at the expected return for every asset in the portfolio.

For MarketXLS as monthly data is utilized, the no. of periods in a year are taken as 12. 

The lowest value among this is the lowest possible return of the portfolio and similarly as the highest.

4. Determining Weights for Every Level of Return in Between:

Quadratic Linear Programming is utilised to minimize portfolio volatility for all different levels of return subject to the constraint that sum of weights equals one. Herein, the optional input regarding the number of data points determines how many points in between the data is calculated for.

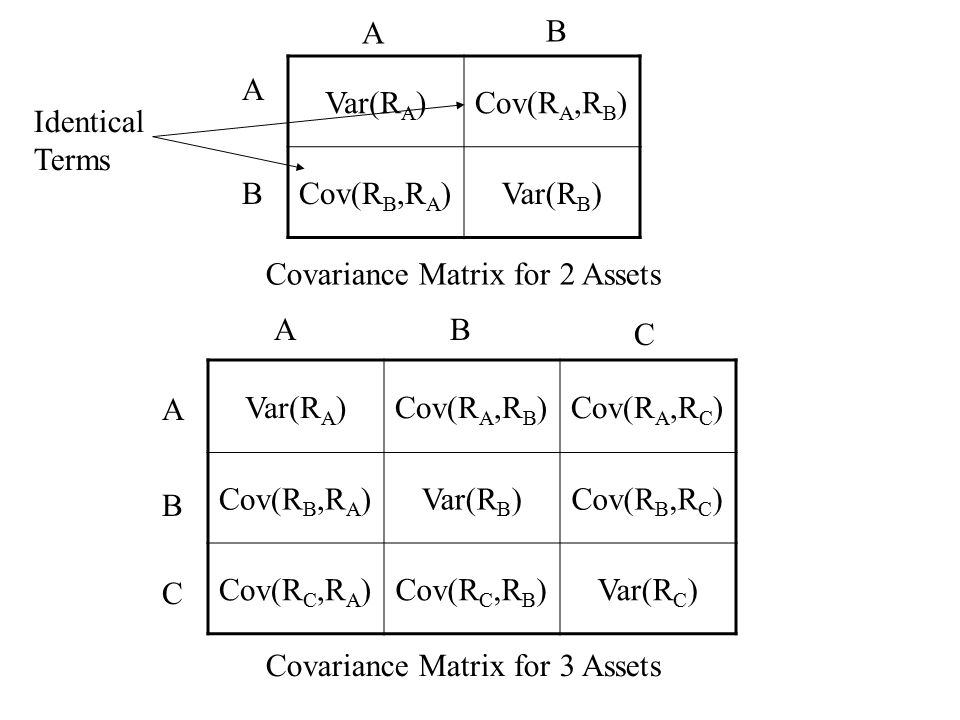
5. Covariance of Portfolio is Calculated:

The covariance matrix is calculated for the portfolio:

Note: This is a two and three asset example and can be done for as many assets as a portfolio might have. 

6. Standard Deviation of Portfolio: 

The portfolio’s standard deviation is calculated below:

Where:

7. Standard Deviation of Portfolio is Annualized:

To maintain consistency in periodicity of different parameters, standard deviation is annualised as follows:

Annualizing Factor = SQRT(Number of Periods a Year)

Note: Since MarketXLS uses monthly values, the annualizing factor is sqrt(12)

For instance, if taking daily data, seeing as a trading year has 252 days, multiply the ratio with the square root of 252.

Similarly,

• for yearly returns, annualizing factor = SQRT(1)
• for monthly returns, annualizing factor = SQRT(12)
• for weekly returns, annualizing factor = SQRT(52)
• for daily returns, annualizing factor = SQRT(252)

8. Plotting the Efficient Frontier:

This results to derive the Efficient frontier plotted with standard deviation (risk) on x-axis and expected return on y-axis. 

The portfolio with lowest risk is plotted as the GMV portfolio. 

The portfolio with the highest Sharpe Ratio is used to plot the Capital Market line as a segment starting at the risk-free-rate of return on the y-axis and extending to the portfolio with the maximum sharpe ratio.  

The investor can use the Efficient frontier of Portfolio excel formula to get a combination of assets that has the optimal level of expected return for a given level of risk as all the portfolios on the line are efficient. An investor can choose a suitable portfolio anywhere on the Efficient Frontier depending on his individual preferences and investment timeframe using MarketXLS.